Ofta ställs man inför frågan hur många olika kombinationer som finns för ett antal objekt. Det kan vara alltifrån chansen att få 7 rätt på lotto eller risken att bli ihjälkörd i trafiken till chansen att med en sexsidig tärning slå först en etta sedan en två sedan en trea fyra femma och en sexa. Eller för att vara korrekt så handlar det i det senare fallet om permutationer som det kallas för istället för kombinationer om ordningen spelar roll.
Antalet möjligheter bestäms naturligtvis av hur många objekt vi ska välja ut, och hur stor den totala mängden är. Vi måste också veta om varje objekt får användas flera gånger eller bara en samt om det spelar någon roll i vilken ordning de kommer.
En riktlinje är att det finns fler kombinationsmöjligheter om ordningen har betydelse, än om den inte har det. Och det finns fler kombinationsmöjlgiheter om man använder sig av repetitioner än om man inte gör det.
Kombinationer utan repetition
Kombinationer utan repetition betyder att varje objekt får användas högst en gång. Då beräknas antalet möjliga sätt att välja ut ”k” antal objekt av totalt ”n” stycken med hjälp av den s.k. binomialkoefficienten Bin(n,k) som ser ut såhär:
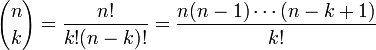
Där n och k alltid är positiva heltal.
Ett exempel:
Antalet möjliga kombinationer att bland 8 personer välja 5 spelare till ett lag:
Så om vi återgår till till de ursprungliga exemplen om chansen att få 7 rätt på lotto och risken att bli ihjälkörd i trafiken.
Antalet kombinationer för en vanlig lottodragning är Bin(35, 7) = 6 724 520 D.v.s. ca 6,7 miljoner kombinationer vilket innebär en chans på 0,15 ppm (parts per million) eller 0,15 på miljonen.
I den svenska trafiken dör ca 420 människor på ett år, av 9,25 miljoner svenskar och risken att dödas i trafiken är 45 ppm eller 45 på miljonen. Risken att dö i trafiken under ett år är alltså 300 gånger större än att tippa sju rätt på lotto. (Då det är ca 300 vardagar under ett år så skulle chanserna på årsbasis bli ungefär lika stora om man lämnade in en lottorad varje vardag under året.)
Kombinationer med repetition
Ofta kan samma objekt förekomma fler gånger och då ökar kombinationsmöjligheterna. Antalet möjligheter att välja ut ”k” objekt ur en mängd med ”n” unika objekt kan beräknas som
n+k-1
( k )
Om man t.ex. slår två sexsidiga tärningar och ska flytta två pjäser enligt tärningarna. Hur många kombinationsmöjligheter finns det för slaget. Eftersom samma resultat kan komma upp mer än en gång handlar det om kombinationer med repetition.
Antalet möjliga slag med tärningarna är
n+k-1 6+2-1
( k ) = ( 2 ) = 7*6 / 2! = 21
Det finns alltså 21 möjliga slag med två tärningar.
Permutationer
permutationer skiljer sig från kombinationer genom att den tar hänsyn till i vilken ordning elementen i urvalet kommer. abc och bca är således inte samma permutation, men samma kombination.
Antalet permutationer av en mängd innehållande n stycken element är n !, där  och utläses ”n-fakultet”.
och utläses ”n-fakultet”.
Detta gäller eftersom det för det första elementet man väljer finns n möjliga val, för nästa element (n-1) element kvar att välja från, för tredje elementet (n-2), osv. till och med det sista elementet som kan ”väljas” på endast ett sätt.
Mängden C = {a,b,c} kan alltså permuteras på 3!=6 sätt: abc, acb, bac, bca, cab, cba.
Antalet möjligheter att välja ut ”r” objekt ur en mängd ”n” objekt med hänsyn till ordningen är:
( n! ) / (n-r)!
För detta har man infört skrivsätten P(n,r), nPr och  .
.
Ibland förekommer samma objekt flera gånger. Då finns det färre möjligheter att arrangera om bokstäverna än om varje objekt är unikt. I själva verket gäller att antalet möjlighetar att arrangera om n bokstäver där några bokstäver förekommer flera gånger är
( n ! ) / (n1! n12! … nk! )
där n1 etc är antal tecken för varje bokstav. Ett exempel: ordet rabarber innehåller 3 r två a två b och ett e. Totalt åtta bokstäver alltså. Antalet möjligheter att arrangera om de åtta bokstäverna i rabarber är alltså
( 8 ! ) / ( 3! 2! 2! 1! ) = 1680
Permutationer med repetition
I en situtation där varje objekt får användas ett obegränsat antal gånger, och där man tar hänsyn till de utvalda objektens ordning kallas permutationer med repetition. Dessa beräknas som
nr
Exempel: Vilken är den minsta längd morsealfabetet, som består av två tecken, lång och kort, som krävs för att klara av det engelska alfabetets 26 bokstäver och tio siffror?
Om man beräknar hur många kombinationer det finns för varje teckenlängd:
ett tecken: 21 = 2 olika möjligheter
två tecken: 22 = 4 olika möjligheter
tre tecken: 23 = 8 olika möjligheter
fyra tecken: 24 = 16 olika möjligheter
fem tecken: 25 = 32 olika möjligheter
För t.ex. en teckenlängd på 4 har vi 2+4+8+16=30 olika möjliga tecken – tillräckligt för alfabetet men för att få med siffror och specialtecken måste vi dock fylla upp med femsiffriga tecken.
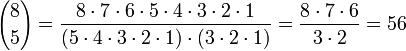
Lämna ett svar